交差検証は機械学習においてトレーニングとテストによるモデル性能の検証を行う際のデータの使い方と言えますが、パラメータチューニングの話と密接な関係があるため分かりにくい部分があると思います。ここでは、交差検証自体の話と実際にどう使うのかを説明しています。
Packages and Datasets
本ページではR version 3.6.1 (2019-07-05)の標準パッケージ以外に以下の追加パッケージを用いています。
| Package | Version | Description |
|---|---|---|
| caret | 6.0.84 | Classification and Regression Training |
| knitr | 1.24 | A General-Purpose Package for Dynamic Report Generation in R |
| psych | 1.8.12 | Procedures for Psychological, Psychometric, and Personality Research |
| tidyverse | 1.2.1 | Easily Install and Load the ‘Tidyverse’ |
また、本ページでは以下のデータセットを用いています。
| Dataset | Package | Version | Description |
|---|---|---|---|
| wbcd | N/A | N/A | Breast Cancer Wisconsin (Diagnostic) Data Set, UCI ML Repository |
交差検証
交差検証(Cross Validation, CV)とは機械学習モデルの性能を評価するための方法の一つです。最適な機械学習パラメータ、例えば最近傍法では近傍数(k)、ナイーブベイズではラプラス推定量を選択する際に用いられます。特にデータの確保が難しい場合に効果を発揮すると言われています。
交差検証の概要
交差検証は Wikipedia では以下のように定義されています。
交差検証とは、統計学において標本データを分割し、その一部をまず解析して、残る部分でその解析のテストを行い、解析自身の妥当性の検証・確認に当てる手法を指す。
注:脚注リンク、括弧書きを削除してあります
トレーニング用データとテスト用データがお互いに交差することから交差検証と呼ばれます。すなわち全てのデータがトレーニング用、テスト用データとして使われるのでトレーニング、テストに偏りがない状態でモデル性能を評価できると言えます。
『Rによる機械学習』の第3章、第4章に出てくるようなデータを二分割して一回のテストで算出された評価指標をモデル性能の検証に利用するホールドアウト検証は交差検証には分類しません。ホールドアウト検証は二分割したデータをそれぞれトレーニング用、テスト用として固定利用します。分割比率には7:3~8:2程度の比率が使わることが一般的です。
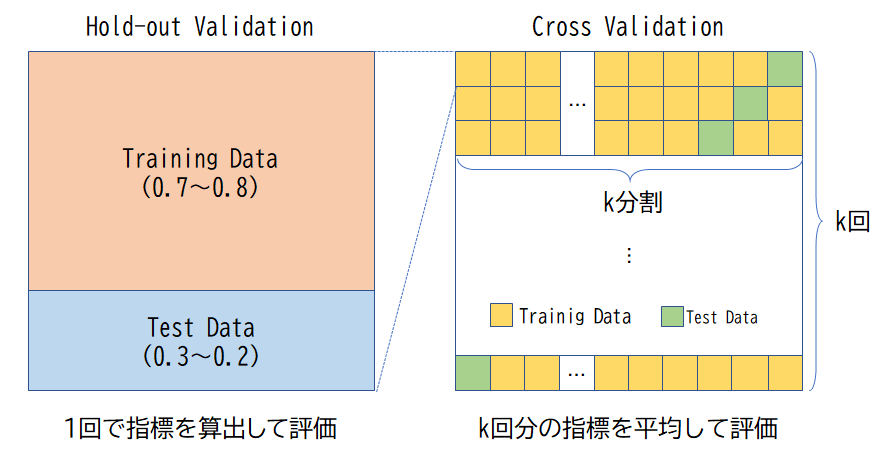
ホールドアウト検証と交差検証
一方、交差検証は対象となるデータを任意に等分割し、トレーニング用データとテスト用データの組み合わせを順次変えて分割数分だけトレーニングとデータを繰り返します。その分、計算量は増えますが、データ全てがトレーニング、テストのどちらにも偏りなく、交差されて使われるのが特徴です。分割数にはk=10が使われることが一般的です。
交差検証におけるモデル性能の評価はk回のテストで算出されたk個の評価指標を平均した値を交差検証の評価指標とします。なお、評価指標については後述します。
交差検証の中で広く知られているものとしては、
- k-fold交差検証(k分割交差検証)
- leave-one-out交差検証(LOO交差検証、一個抜き交差検証)
の二つがあります。上記以外にも様々な交差検証があります。
k-fold交差検証
k-fold交差検証(k分割交差検証)はデータをk分割し、分割したデータの一つ(k1)をテスト用に残り(k2,3,...)をトレーニング用に用いてモデル性能を評価します。続いて先程とは異なる分割したデータ(k2)をテスト用に残り(k1,3,...)をトレーニング用に用いてモデル性能を評価します。このような評価を分割数(k)回繰り返し、求められたk個の評価結果を平均することで最終的な評価とします。
k-fold交差検証(k分割交差検証)のイメージは 機械学習モデルの性能評価入門!交差検証(クロスバリデーション)とは を参照してください。
leave-one-out交差検証
leave-one-out交差検証(LOO交差検証)はn個データから1個だけ抜き出しテスト用データに、残りのn−1個のデータでトレーニングを行います。これをn回(データの個数分)繰り返しモデル性能の評価を行います。k-fold交差検証でk=nにした場合と同等ですが、データ数に比例した計算コストがかかるのが難点です。
評価指標
評価指標とは文字通りモデルの性能を評価するための指標です。最近傍法やナイーブベイズなどの分類(classification)アルゴリズムにおいては、混同行列に基づく評価指標を用います。
混同行列
混同行列(Confusion Matrix)とは以下のような分類結果をまとめたクロス集計表のことです。混同行列を用いることで機械学習のモデルがどのようなモデル性能を持っているかが分かります。
ちなみに混同行列は疾病の検査に関わる調査に起因してるようで陽性(Positive)、陰性(Negative)で分類されています。適期、自分が分かりやすい言葉に置き換えて考えると理解しやすくなるかもしれません。
| Predict/Actual | Actual Posivive | Actual Negative |
|---|---|---|
| Pridect Positive | TP(True Positive・真陽性) | FP(False Positive・偽陽性・第一種の過誤) |
| Pridect Negative | FN(False Negative・偽陰性・第二種の過誤) | TN(True Negative・真陽性) |
上記の混同行列は二値分類(二項分類)の場合です。多値分類の場合は行列の各方向に分類項目が増えるだけで考え方は同様です。混同行列の書き方には「Pridect/Actual」を「Actual/Predict」と転置させた書き方もありますので注意してください。
この混同行列を利用してモデル性能を判定するための様々な評価指標が定義されています。
評価指標の定義
評価指標は分類の目的に応じた評価ができるように様々な指標が定義されています。例えば『Rによる機械学習』の第4章で出てくるスパムフィルの場合、正しく分類できる割合が高い方がモデル性能が高いと言えます。一方、同書の第3章に出てくるがん細胞分類の場合、正しく分類できる割合が高いとしても「がん細胞を正常細胞と誤分類」してしまう割合が高いとがん患者を放置することになるためスパムフィルタとは異なる評価指標でモデルを評価する必要があることが分かります。
主な評価指標には以下のようなものがあります。
| 評価指標 | 定義式 | 備考 |
|---|---|---|
| 正確度(ACC) | TP+TNTP+FN+FP+TN | Accuracy・Acc・正解率 |
| 誤り率(ER) | FN+FPTP+FN+FP+TN | Error Rate |
| 真陽性率(TPR) | TPTP+FN | True Positive Rate・再現率(Recall)・感度(Sensitivity) |
| 真陰性率(TNR) | TNFP+TN | True Negative Rate・特異度(Specificity) |
| 偽陽性率(FPR) | FPFP+TN | False Positive Rate・Fall-out |
| 偽陰性率(FNR) | FNTP+FN | False Negative Rate・Miss rate |
| 陽性的中率(PPV) | TPTP+FP | Positive Predictive Value・適合率・精度(Precision) |
| 陰性的中率(NPV) | TNFN+TN | Negative Predictive Value |
| 偽発見率1(FDR) | FPTP+FP | False Discovery Rate |
| 誤脱落率2(FOR) | FNFN+TN | False Omission Rate |
| 陽性尤度比(LR+) | TPRFPR | Positive Likelihood Ratio・PLR |
| 陰性尤度比(LR-) | FNRTNR | Negative Likelihood Ratio・NLR |
| 診断オッズ比(DOR) | LR+LR− | Diagnostic Odds Ratio |
| 調和平均(F1) | 2×PPV×TPRPPV+TPR | F値(F-score)・F尺度(F-measure) |
| BER | 1−12×(TPR+TNR) | Balance Error Rate |
1 「誤」発見ではなく「偽」発見が一般的のようです
2 適切な日本語が不明のため直訳しています
では、主な評価指標を簡単に解説します。
正確度・誤答率(エラーレート)
正確度(Accuracy・ACC)は全データに対して正しく分類した割合です。
最も基本的な評価指標であり正確度とも呼ばれます。精度と呼ぶ人もいるようですが、精度(Precision)は陽性的中率(PPV)の別名として使わることが多いので、どちらの意味で利用されているのかに注意してください。
定義式から分かるように1に近いほど正確度が高い、すなわち、より正しく分類されているということになります。一方、誤答率(エラーレート)は正確度の逆で対象を正しく分類できなかった割合です。正確度とは以下の関係があります。
正確度(ACC)=TP+TNTP+FN+FP+TN=1−誤答率(ER)
真陽性率・偽陰性率
真陽性率(TPR),偽陰性率(FNR)は実際に陽性であるデータに対する割合です。
真陽性率は実際に陽性のデータを陽性であると分類した割合です。感度(Sensitive)や再現率(Recall)とも呼ばれます。定義式から分かるように1に近いほど陽性のデータが正しく分類されているということになります。
偽陰性率は実際に陰性のデータが陽性であると分類した割合です。ミスレート(Miss rate)とも呼ばれます。定義式から分かるように0に近いほど陰性のデータが正しく分類されているということになります。
真陽性率と偽陰性率との間には以下の関係があります。
真陽性率(TPR)=TPTP+FN=1−FNTP+FN=1−偽陰性率(FNR)
真陰性率・偽陽性率
真陰性率(TNR),偽陽性率(FPR)は実際に陰性であるデータに対する割合です。
真陰性率は実際に陰性のデータを陰性であると分類した割合です。特異度(Specificity)とも呼ばれます。定義式から分かるように1に近いほど陰性のデータが正しく分類されているということになります。
偽陽性率は実際に陽性のデータを陰性であると分類した割合です。フォールアウト(Fall-out)とも呼ばれます。定義式から分かるように0に近いほど陽性のデータが正しく分類されているということになります。
真陰性率と偽陽性率との間には以下の関係があります。
真陰性率(TNR)=TNFP+TN=1−FPFP+TN=1−偽陽性率(FPR)
陽性的中率・偽発見率
陽性的中率(PPV),偽発見率(FDR)は陽性であると分類されたデータに対する割合です。
陽性的中率は陽性と分類されたデータの中で実際に陽性だったデータの割合です。適合率・精度(Precision)とも呼ばれます。定義式から分かるように1に近いほど正しく分類されているということになります。
偽発見率は陽性と分類されたデータの中で実際には陰性だったデータの割合です。定義式から分かるように0に近いほど正しく分類されているということになります。
陽性的中率(PPV)=TPTP+FP=1−FPTP+FP=1−偽発見率(FDR)
調和平均(F1)
調和平均(F1)とは「逆数の平均の逆数」と定義されており、機械学習のおいては適合率(陽性的中率・精度)と再現率(真陽性率・感度)を用いた指標です。
112(1PPV+1TPR)=112(PPV+TPRPPV×TPR)=2×PPV×TPRPPV+TPR
適合率は「陽性と分類されたデータの中で実際に陽性だったデータの割合」なので正確性の指標の一つです。一方、再現率は「実際に陽性のデータを陽性であると分類した割合」なので網羅性の指標の一つです。
適合率=TPTP+FPを上げる(FPを減らす)と再現率(TPTP+FN)が下がる(FNが増える)というトレードオフの傾向があるため、適合率(正確性の指標)と再現率(網羅性の指標)のバランスを取りたい時に用いる指標です。
BER
BER(Balance Error Rate)は偽陽性率と偽陰性率のバランスを取りたい場合に用いる指標で、誤分類の調和平均と言えます。
12(FPR+FNR)=12(FPFP+TN+FNTP+FN) =1−12(TPR+TNR)=1−12(TPTP+FN+TNFP+TN)
実際の交差検証
交差検証はモデルの最適パラメータの選定する際に使われます。ここでは『Rによる機械学習』の第3章で使われている サンプルデータ を用いて交差検証により最近傍法の最適パラメータ(k)を求めてみます。
使用するデータは ウィスコンシン州のがん検診データ で、『Rによる機械学習』の原著作者が 加工したデータ を用いています。
wbcd| diagnosis | radius_mean | texture_mean | perimeter_mean | area_mean | smoothness_mean | compactness_mean | concavity_mean | points_mean | symmetry_mean | dimension_mean | radius_se | texture_se | perimeter_se | area_se | smoothness_se | compactness_se | concavity_se | points_se | symmetry_se | dimension_se | radius_worst | texture_worst | perimeter_worst | area_worst | smoothness_worst | compactness_worst | concavity_worst | points_worst | symmetry_worst | dimension_worst | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | B | 0.25 | 0.09 | 0.24 | 0.14 | 0.45 | 0.15 | 0.09 | 0.18 | 0.45 | 0.2 | 0.05 | 0.07 | 0.04 | 0.02 | 0.22 | 0.07 | 0.04 | 0.24 | 0.16 | 0.05 | 0.2 | 0.1 | 0.18 | 0.09 | 0.44 | 0.1 | 0.1 | 0.32 | 0.25 | 0.08 |
| 2 | B | 0.17 | 0.31 | 0.18 | 0.09 | 0.4 | 0.29 | 0.15 | 0.13 | 0.44 | 0.31 | 0.12 | 0.18 | 0.13 | 0.04 | 0.2 | 0.25 | 0.08 | 0.26 | 0.38 | 0.08 | 0.14 | 0.29 | 0.14 | 0.06 | 0.33 | 0.22 | 0.15 | 0.27 | 0.27 | 0.14 |
| 3 | B | 0.19 | 0.24 | 0.19 | 0.1 | 0.5 | 0.18 | 0.07 | 0.12 | 0.33 | 0.28 | 0.03 | 0.23 | 0.03 | 0.01 | 0.12 | 0.05 | 0.03 | 0.14 | 0.13 | 0.05 | 0.16 | 0.38 | 0.15 | 0.07 | 0.43 | 0.12 | 0.09 | 0.26 | 0.28 | 0.16 |
| … | NA | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 567 | M | 0.39 | 0.43 | 0.38 | 0.24 | 0.34 | 0.26 | 0.13 | 0.16 | 0.34 | 0.28 | 0.03 | 0.03 | 0.03 | 0.02 | 0.05 | 0.09 | 0.04 | 0.11 | 0.05 | 0.06 | 0.35 | 0.43 | 0.32 | 0.19 | 0.39 | 0.29 | 0.29 | 0.42 | 0.32 | 0.28 |
| 568 | B | 0.36 | 0.14 | 0.35 | 0.21 | 0.52 | 0.22 | 0.16 | 0.32 | 0.3 | 0.24 | 0.07 | 0.08 | 0.07 | 0.04 | 0.15 | 0.08 | 0.04 | 0.22 | 0.2 | 0.09 | 0.28 | 0.13 | 0.26 | 0.14 | 0.42 | 0.12 | 0.11 | 0.37 | 0.21 | 0.15 |
| 569 | M | 0.68 | 0.18 | 0.67 | 0.53 | 0.43 | 0.41 | 0.45 | 0.62 | 0.46 | 0.25 | 0.08 | 0.21 | 0.08 | 0.06 | 0.09 | 0.18 | 0.09 | 0.25 | 0.12 | 0.12 | 0.53 | 0.26 | 0.51 | 0.33 | 0.32 | 0.25 | 0.32 | 0.68 | 0.23 | 0.21 |
なお、データには最小最大正規化の処理を適用してあります。また、因子の水準の順序が『Rによる機械学習』のサンプルコードとは異なり“M”(悪性)、“B”(良性)の順になっている点に注意してください。
まず、最初に必要なパッケージを読み込みます。交差検証などに使うcaretパッケージも同時に読み込んでおきます。
library(caret)
library(tidyverse)
データの分割
『Rによる機械学習』第3章のサンプルコード同様にトレーニング用データとテスト用データに分割しておきます。
wbcd_train <- wbcd[1:469, ]
wbcd_test <- wbcd[470:569, ]ホールド・アウト検証による評価
『Rによる機械学習』第3章のサンプルコード同様にホールド・アウト検証による評価をしておきます。最近傍法のパラメータ(k)はサンプルコード同様にトレーニング用データ数の平方根(k = 21)としています。なお、最近傍法にはcaret::knn3Train関数を用います。caret::knn3Trainの返り値は文字型なのでクロス集計のため因子型への変換を行っています。
set.seed(123)
ho_result <- caret::knn3Train(train = wbcd_train[, -1], test = wbcd_test[, -1],
cl = wbcd_train[, 1], k = 21) %>%
as.factor() %>% forcats::fct_relevel("M") %>%
caret::confusionMatrix(reference = wbcd_test$diagnosis)
ho_result## Confusion Matrix and Statistics
##
## Reference
## Prediction M B
## M 37 0
## B 2 61
##
## Accuracy : 0.98
## 95% CI : (0.9296, 0.9976)
## No Information Rate : 0.61
## P-Value [Acc > NIR] : <2e-16
##
## Kappa : 0.9576
##
## Mcnemar's Test P-Value : 0.4795
##
## Sensitivity : 0.9487
## Specificity : 1.0000
## Pos Pred Value : 1.0000
## Neg Pred Value : 0.9683
## Prevalence : 0.3900
## Detection Rate : 0.3700
## Detection Prevalence : 0.3700
## Balanced Accuracy : 0.9744
##
## 'Positive' Class : M
##
モデル評価の結果、「正確度(Accuracy) =0.98、真陽性率(Sensitivity) =0.9487179」となっており、残念ながら偽陰性が5.1%ほど出ています。
交差検証
caret::train関数を用いて交差検証(cv)によりk近傍法(knn)における最適な近傍数(k)を1〜20の範囲から求めてみます。以降、常に結果が同じになるように乱数シードを指定しています。
set.seed(123)
train_result <- wbcd_train %>%
caret::train(diagnosis ~ ., data = ., method = "knn",
tuneGrid = expand.grid(k = c(1:20)),
trControl = caret::trainControl(method = "cv"))
train_result## k-Nearest Neighbors
##
## 469 samples
## 30 predictor
## 2 classes: 'M', 'B'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 422, 422, 423, 422, 421, 422, ...
## Resampling results across tuning parameters:
##
## k Accuracy Kappa
## 1 0.9553134 0.9031275
## 2 0.9595205 0.9128038
## 3 0.9659073 0.9256349
## 4 0.9680793 0.9306694
## 5 0.9659073 0.9257318
## 6 0.9702089 0.9348913
## 7 0.9744642 0.9443481
## 8 0.9744642 0.9442407
## 9 0.9744180 0.9440507
## 10 0.9679887 0.9301264
## 11 0.9744180 0.9439333
## 12 0.9722441 0.9393240
## 13 0.9722903 0.9395140
## 14 0.9701627 0.9347651
## 15 0.9701164 0.9346762
## 16 0.9701164 0.9346762
## 17 0.9679887 0.9299273
## 18 0.9659054 0.9252251
## 19 0.9637778 0.9205773
## 20 0.9573023 0.9068185
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was k = 8. デフォルトの分割数は10なので、kの値一つあたり10回のトレーニング、テストを行い評価指標を算出しています。最終行にあるように正確度(Accuracy)を評価指標として最適モデルを選定した結果 k =8 を使っているモデルが最適となりました。
正確度(Accuracy)とkの値をプロットすると以下のようになり、kがある程度の値までは正確度が比例して上がり、ある程度を越えると反比例する傾向があることがわかります。
plot(train_result)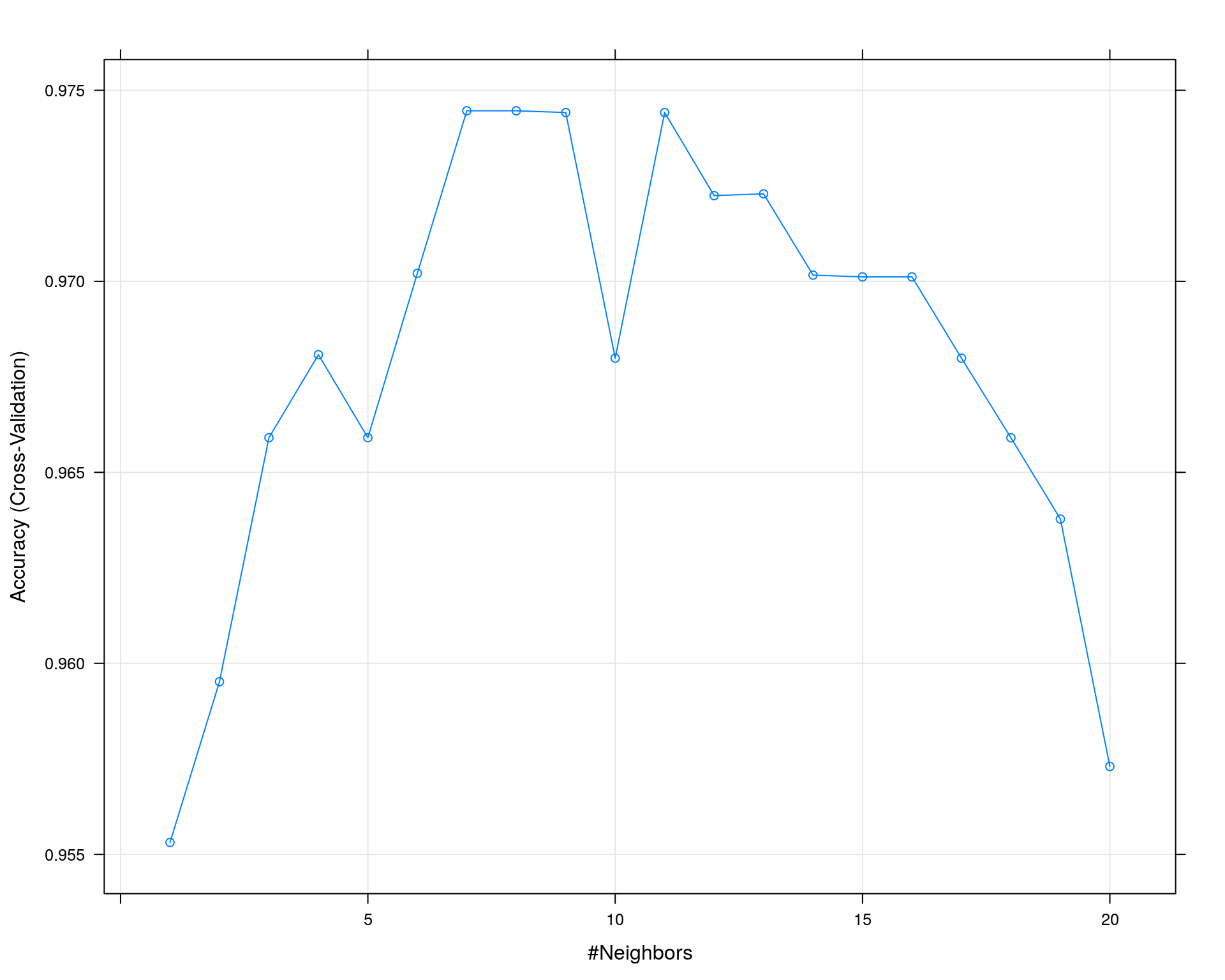
では、この値(k =8)でテスト用データを用いて最終評価をしてみます。
paste0("k = ", train_result$bestTune$k)## [1] "k = 8"set.seed(123)
caret::knn3Train(train = wbcd_train[, -1], test = wbcd_test[, -1],
cl = wbcd_train[, 1], k = train_result$bestTune$k) %>%
as.factor() %>% forcats::fct_relevel("M") %>%
caret::confusionMatrix(reference = wbcd_test$diagnosis)## Confusion Matrix and Statistics
##
## Reference
## Prediction M B
## M 36 0
## B 3 61
##
## Accuracy : 0.97
## 95% CI : (0.9148, 0.9938)
## No Information Rate : 0.61
## P-Value [Acc > NIR] : <2e-16
##
## Kappa : 0.9361
##
## Mcnemar's Test P-Value : 0.2482
##
## Sensitivity : 0.9231
## Specificity : 1.0000
## Pos Pred Value : 1.0000
## Neg Pred Value : 0.9531
## Prevalence : 0.3900
## Detection Rate : 0.3600
## Detection Prevalence : 0.3600
## Balanced Accuracy : 0.9615
##
## 'Positive' Class : M
## 正確度(Accuracy)を評価指標に用いたデフォルトの交差検証ではk =21のホールドアウト検証に比べると偽陰性が増えています。
評価指標の指定
caret::train関数は前述のようにデフォルトでは正確度(Accuracy)を用いて評価します。これは評価指標を計算するサマリ関数としてcaret::defaultSummary関数が呼び出されているからです。
wbcd_train %>%
caret::train(diagnosis ~ ., data = ., method = "knn",
tuneGrid = expand.grid(k = c(1:20)),
trControl = caret::trainControl(method = "cv",
summaryFunction = caret::defaultSummary,
classProbs = FALSE),
metric = "Accuracy") caret::defaultSummary関数を他の関数にすれば評価指標を変更することができます。caretパッケージには二値分割(二項分割)の評価のために以下のサマリ関数が用意されています。
| Summary Function | 正確度 | κ係数 | 再現率 | 特異度 | 適合率 | 調和平均 |
|---|---|---|---|---|---|---|
defaultSummary |
x | x | ||||
towClassSummary |
x | x | ||||
prSummary |
x | x | x |
では、適合率(Precision、陽性的中率・PPV)を用いて交差検証を行ってみます。
set.seed(123)
train_result <- wbcd_train %>%
caret::train(diagnosis ~ ., data = ., method = "knn",
tuneGrid = expand.grid(k = c(1:20)),
trControl = caret::trainControl(method = "cv",
summaryFunction = caret::prSummary,
classProbs = TRUE),
metric = "Precision")
train_result## k-Nearest Neighbors
##
## 469 samples
## 30 predictor
## 2 classes: 'M', 'B'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 422, 422, 423, 422, 421, 422, ...
## Resampling results across tuning parameters:
##
## k AUC Precision Recall F
## 1 0.04947661 0.9530964 0.9248366 0.9380534
## 2 0.10172092 0.9609671 0.9310458 0.9446455
## 3 0.13727293 0.9826797 0.9251634 0.9519880
## 4 0.15635529 0.9777090 0.9366013 0.9555080
## 5 0.17081611 0.9769247 0.9307190 0.9521548
## 6 0.20317425 0.9818954 0.9366013 0.9578836
## 7 0.22535773 0.9818954 0.9483660 0.9641336
## 8 0.25414993 0.9885621 0.9428105 0.9639309
## 9 0.27751957 0.9881944 0.9424837 0.9637476
## 10 0.29475712 0.9826389 0.9310458 0.9548349
## 11 0.30195168 0.9937500 0.9366013 0.9635744
## 12 0.32512944 0.9881944 0.9366013 0.9607173
## 13 0.33691651 0.9885621 0.9369281 0.9609006
## 14 0.35379017 0.9885621 0.9313725 0.9576921
## 15 0.38751520 0.9881944 0.9310458 0.9576921
## 16 0.39270072 0.9881944 0.9310458 0.9576921
## 17 0.39909278 0.9881944 0.9254902 0.9544835
## 18 0.39952477 0.9881944 0.9199346 0.9512750
## 19 0.40528510 0.9881944 0.9143791 0.9482498
## 20 0.40415079 0.9759722 0.9084967 0.9397129
##
## Precision was used to select the optimal model using the largest value.
## The final value used for the model was k = 11.plot(train_result)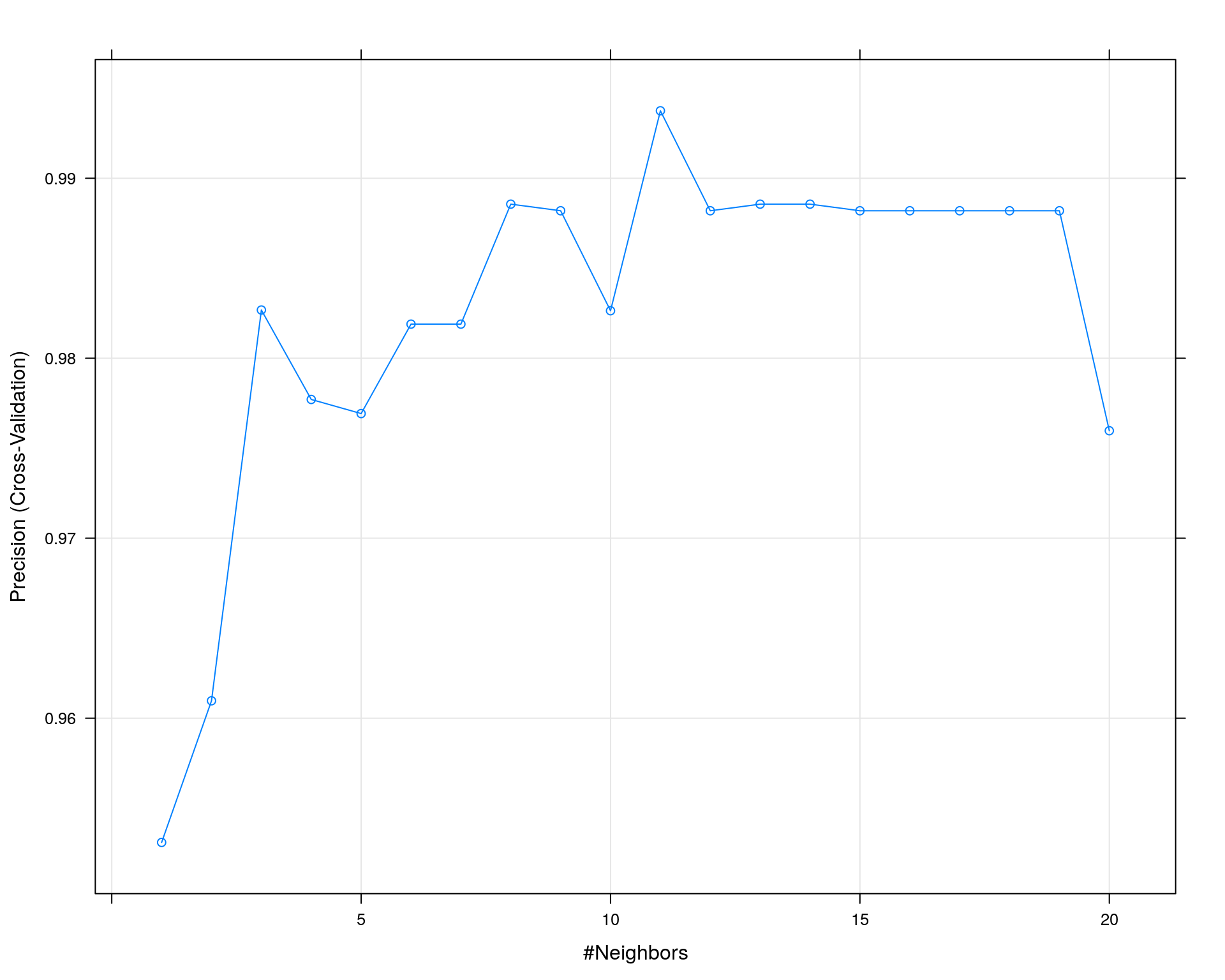
paste0("k = ", train_result$bestTune$k)## [1] "k = 11"set.seed(123)
caret::knn3Train(train = wbcd_train[, -1], test = wbcd_test[, -1],
cl = wbcd_train[, 1], k = train_result$bestTune$k) %>%
as.factor() %>% forcats::fct_relevel("M") %>%
caret::confusionMatrix(reference = wbcd_test$diagnosis)## Confusion Matrix and Statistics
##
## Reference
## Prediction M B
## M 36 0
## B 3 61
##
## Accuracy : 0.97
## 95% CI : (0.9148, 0.9938)
## No Information Rate : 0.61
## P-Value [Acc > NIR] : <2e-16
##
## Kappa : 0.9361
##
## Mcnemar's Test P-Value : 0.2482
##
## Sensitivity : 0.9231
## Specificity : 1.0000
## Pos Pred Value : 1.0000
## Neg Pred Value : 0.9531
## Prevalence : 0.3900
## Detection Rate : 0.3600
## Detection Prevalence : 0.3600
## Balanced Accuracy : 0.9615
##
## 'Positive' Class : M
## 適合率(Precision)を評価指標に用いた結果、正確度(Accuracy)を用いて交差検証した結果と比べて偽陰性(FN)、偽陽性(FP)共に変化はありませんが、適合率(Precision)はkの値が増えると収束する傾向があるようです。
サマリ関数を定義する
では、caretパッケージにて用意されているサマリ関数で定義されていない真陽性率(TPR)・真陰性率(TNR)・偽陽性率(FPR)・偽陰性率(FNR)などを評価指標を利用する場合にはどのようにすれば良いでしょうか。
結論から言うとサマリ関数を自分で定義する必要があります。ただし、caret::trControl関数はサマリ関数の返り値が最大値のものを選択しますので、偽陽性率や偽陰性率のように0に近いほど良いと判断する評価指標を利用するには注意が必要です。
orgSummary <- function (data, lev = NULL, model = NULL) {
if (is.character(data$obs)) {
data$obs <- factor(data$obs, levels = lev) # 文字の場合、因子化
}
conf.mat <- table(data$pred, data$obs) # 混同行列の作成
fpr <- conf.mat[1, 2] / sum(conf.mat[, 2]) # 偽陽性率
tnr <- 1 - fpr # 真陰性率
fnr <- conf.mat[2, 1] / sum(conf.mat[, 1]) # 偽陰性率
tpr <- 1 - fnr # 真陽性率
# `trainControl`関数の選択基準(`selectionFunction`)は"best"(最大値)か
# "oneSE"しか選べないため、より小さい値を選択したい偽陽性率、偽陰性率では
# 評価されませんので、それらを1から引いた真陰性率、真陽性率を使います。
ret <- c('TPR' = tpr, 'FNR(1-TPR)' = fnr, 'TNR' = tnr, 'FPR(1-TNR)' = fpr)
return(ret) # 計算結果を返す
} サマリ関数を定義しましたので、偽陰性率(FNR)で交差検証を行ってみます。caret::train関数は前述の通りサマリ関数の返り値が最大値になるパラメータを選択しますので、ここでは真陽性率(TPR = 1 - FNR)を評価指標として指定します。
set.seed(123)
train_result <- wbcd_train %>%
caret::train(diagnosis ~ ., data = ., method = "knn",
tuneGrid = expand.grid(k = c(1:20)),
trControl = caret::trainControl(method = "cv",
summaryFunction = orgSummary,
classProbs = TRUE),
metric = "TPR")
train_result## k-Nearest Neighbors
##
## 469 samples
## 30 predictor
## 2 classes: 'M', 'B'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 422, 422, 423, 422, 421, 422, ...
## Resampling results across tuning parameters:
##
## k TPR FNR(1-TPR) TNR FPR(1-TNR)
## 1 0.9248366 0.07516340 0.9731034 0.026896552
## 2 0.9310458 0.06895425 0.9764368 0.023563218
## 3 0.9251634 0.07483660 0.9898851 0.010114943
## 4 0.9366013 0.06339869 0.9865517 0.013448276
## 5 0.9307190 0.06928105 0.9865517 0.013448276
## 6 0.9366013 0.06339869 0.9898851 0.010114943
## 7 0.9483660 0.05163399 0.9898851 0.010114943
## 8 0.9428105 0.05718954 0.9932184 0.006781609
## 9 0.9424837 0.05751634 0.9932184 0.006781609
## 10 0.9310458 0.06895425 0.9897701 0.010229885
## 11 0.9366013 0.06339869 0.9965517 0.003448276
## 12 0.9366013 0.06339869 0.9931034 0.006896552
## 13 0.9369281 0.06307190 0.9931034 0.006896552
## 14 0.9313725 0.06862745 0.9931034 0.006896552
## 15 0.9310458 0.06895425 0.9931034 0.006896552
## 16 0.9310458 0.06895425 0.9931034 0.006896552
## 17 0.9254902 0.07450980 0.9931034 0.006896552
## 18 0.9199346 0.08006536 0.9931034 0.006896552
## 19 0.9143791 0.08562092 0.9931034 0.006896552
## 20 0.9084967 0.09150327 0.9863218 0.013678161
##
## TPR was used to select the optimal model using the largest value.
## The final value used for the model was k = 7.plot(train_result)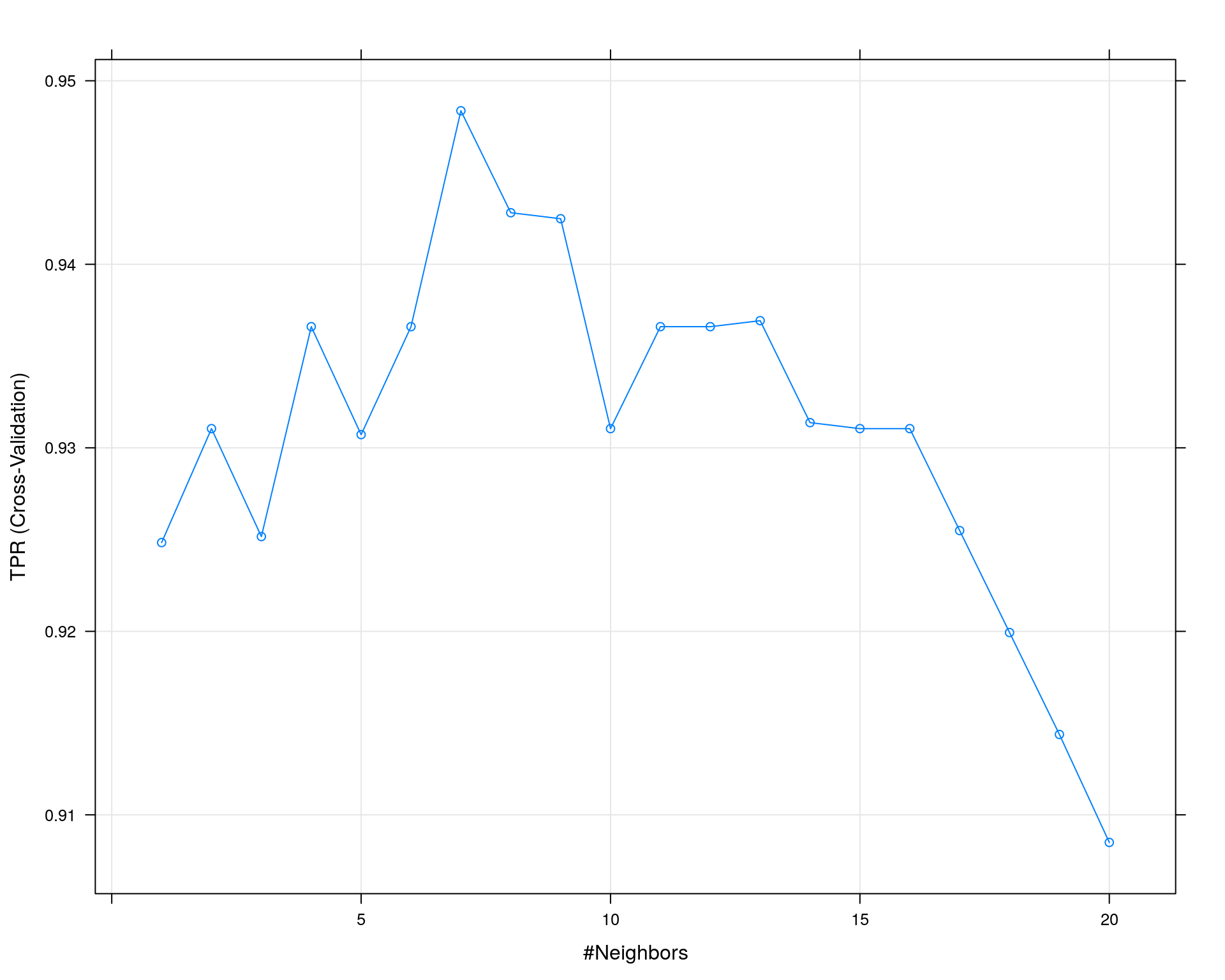
paste0("k = ", train_result$bestTune$k)## [1] "k = 7"set.seed(123)
caret::knn3Train(train = wbcd_train[, -1], test = wbcd_test[, -1],
cl = wbcd_train[, 1], k = train_result$bestTune$k) %>%
as.factor() %>% forcats::fct_relevel("M") %>%
caret::confusionMatrix(reference = wbcd_test$diagnosis)## Confusion Matrix and Statistics
##
## Reference
## Prediction M B
## M 35 0
## B 4 61
##
## Accuracy : 0.96
## 95% CI : (0.9007, 0.989)
## No Information Rate : 0.61
## P-Value [Acc > NIR] : 2.387e-16
##
## Kappa : 0.9143
##
## Mcnemar's Test P-Value : 0.1336
##
## Sensitivity : 0.8974
## Specificity : 1.0000
## Pos Pred Value : 1.0000
## Neg Pred Value : 0.9385
## Prevalence : 0.3900
## Detection Rate : 0.3500
## Detection Prevalence : 0.3500
## Balanced Accuracy : 0.9487
##
## 'Positive' Class : M
## 真陽性率(TPR)を評価指標に用いた結果、期待とは裏腹に偽陰性(FN)が増える結果となりました。
まとめ
(二値分類の)交差検証には様々な評価指標があります。評価指標を変えることでパラメータの最適値(最適モデル)も変わることから目的にあった評価指標を用いて交差検証を行う必要があります。
参考資料
- モデルの汎化性を評価する「交差検証」について、Pythonで学んでみた
- 交差検証
- Confusion matrix(混同行列)
- 機械学習の評価指標
- 「診断精度研究のメタ分析」の入門
- scikit-learn でクラス分類結果を評価する
- 検索性能の評価
Enjoy!