クロス集計した任意の二変量のデータの分布を比較するにはχ2分布を用いた適合度の検定がありますが、ヒストグラムのような度数分布形状を直接的に比較するにはQQプロットを用いて可視化しながら比較する方法が分かりやすいと思います。QQプロットは正規分布か否かを確認する正規QQプロットのような確率分布との比較に使われるプロットですが R のqqplot関数は任意の二変量を比較することが可能です。
なお、文中に出てくる検定に関しては有意水準(α)は 5% で判定を行っています。
Packages and Datasets
本ページではR version 3.4.4 (2018-03-15)の標準パッケージ以外に以下の追加パッケージを用いています。
| Package | Version | Description |
|---|---|---|
| GGally | 1.4.0 | Extension to ‘ggplot2’ |
| ggplot2 | 3.1.0 | Create Elegant Data Visualisations Using the Grammar of Graphics |
| knitr | 1.20 | A General-Purpose Package for Dynamic Report Generation in R |
| tidyverse | 1.2.1 | Easily Install and Load the ‘Tidyverse’ |
また、本ページでは以下のデータセットを用いています。
| Dataset | Package | Version | Description |
|---|---|---|---|
| iris | datasets | 3.4.4 | Edgar Anderson’s Iris Data |
はじめに
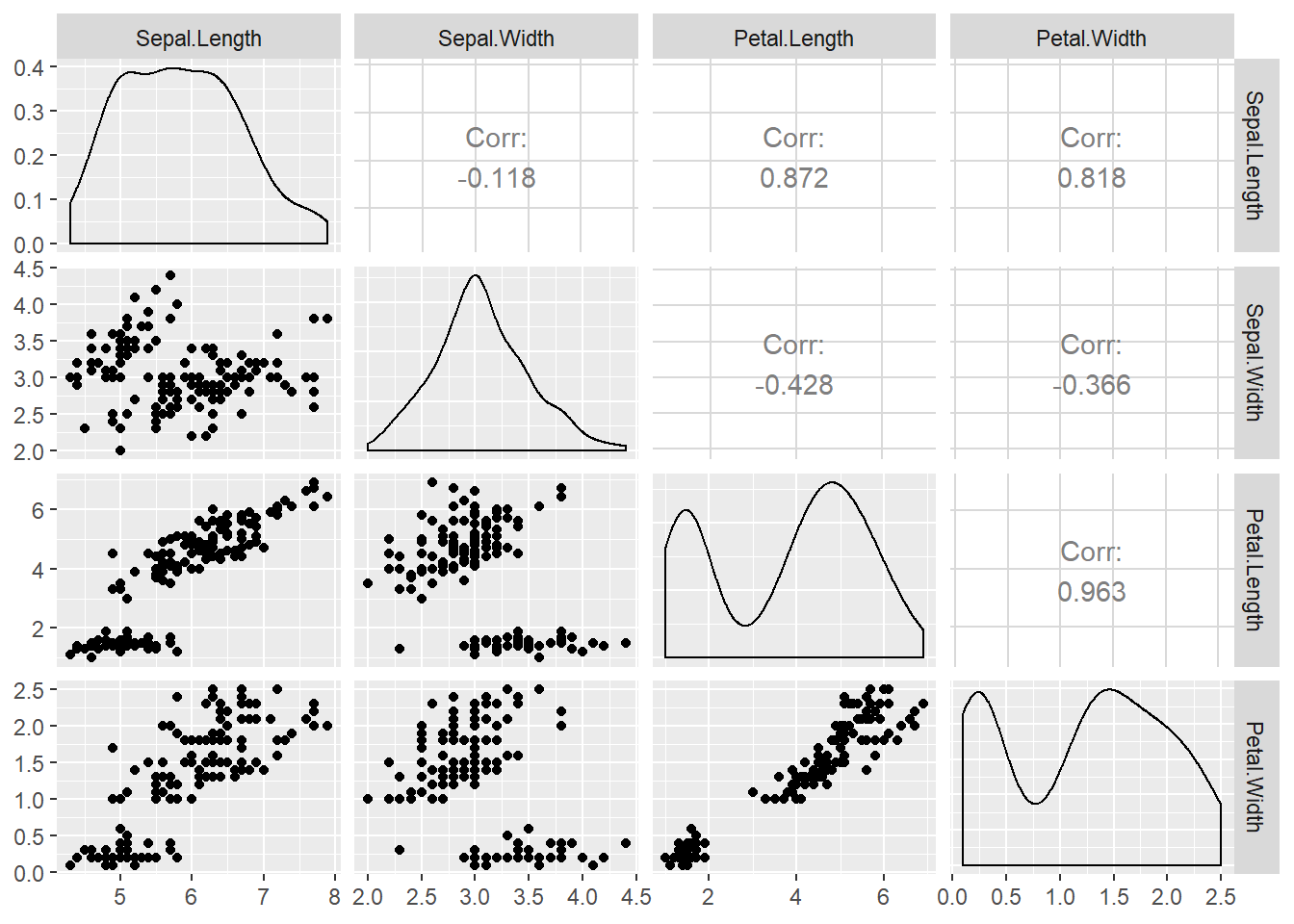
比較の対象となるirisデータセットは下図のような分布をしています。
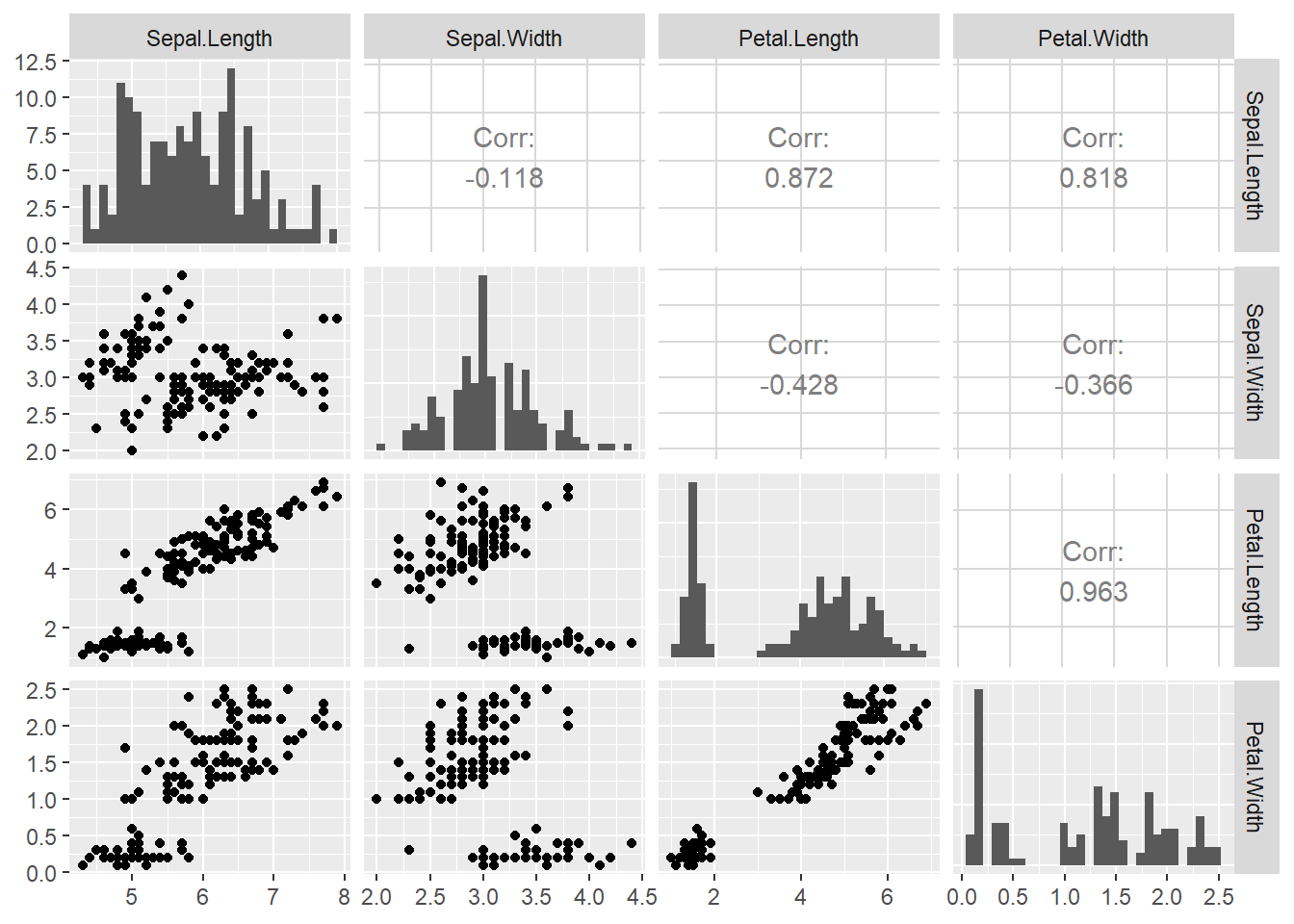
「Sepal.LengthとSepal.Width」、「Petal.LengthとPetal.Width」の分布(グラフの対角線上)が似ているように見えますが、同様の分布と言っても差し支えないでしょうか?QQプロットを利用して確認してみます。
QQプロットで比較する
QQプロットは任意のデータ分布と任意の確率分布が等しいかどうかを確認する際に使われるグラフです。よく利用されるのは任意のデータ分布が正規分布と見なせるか否かを判定する場合です。例えば、以下のirisデータセットのSepal.Widthデータに対する正規QQプロットを描いてみると。
iris %>% dplyr::select(Sepal.Width) %>%
GGally::ggpairs(diag = list(continuous = "barDiag"), progress = FALSE)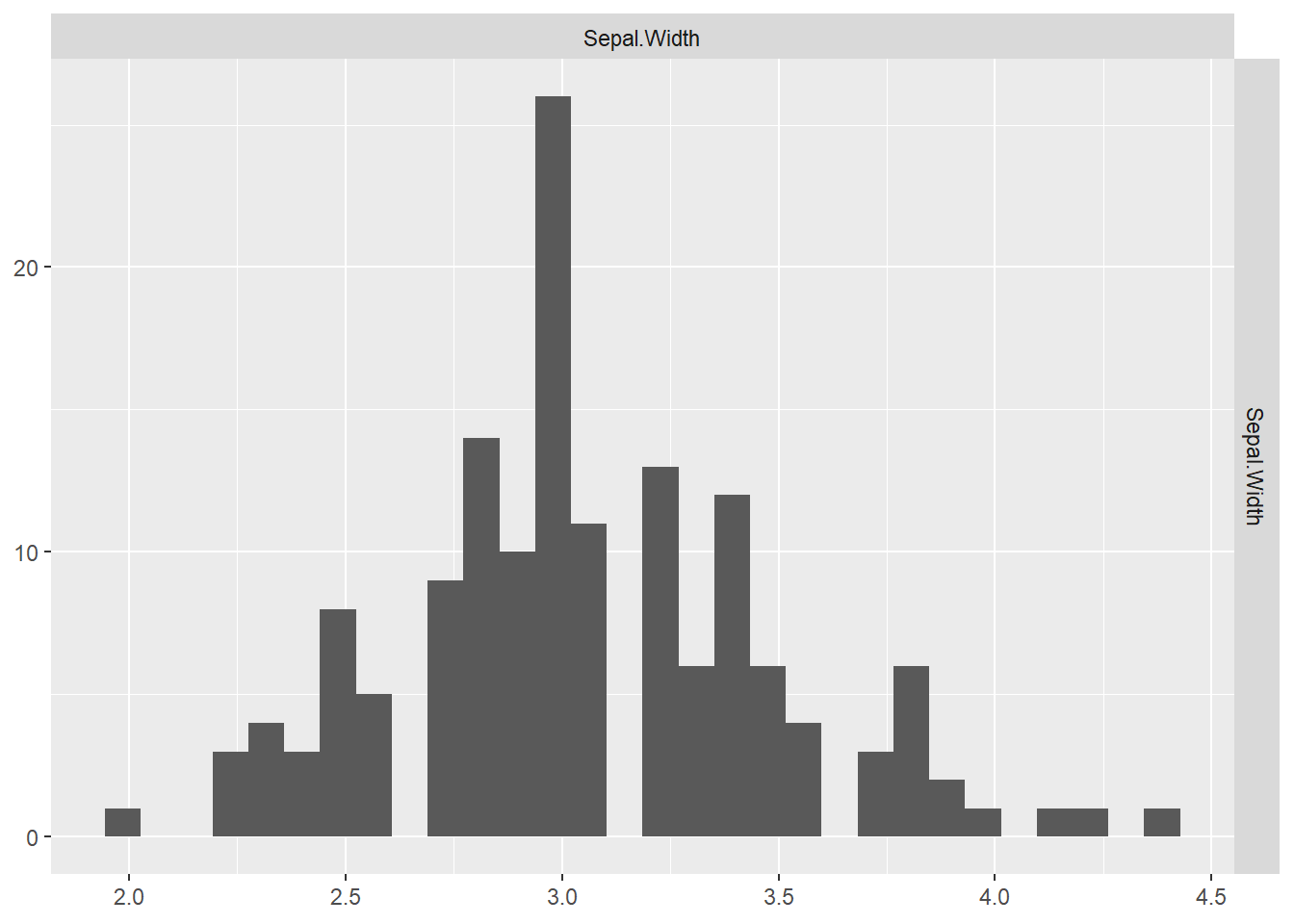
iris %>% with(., qqnorm(y = Sepal.Width))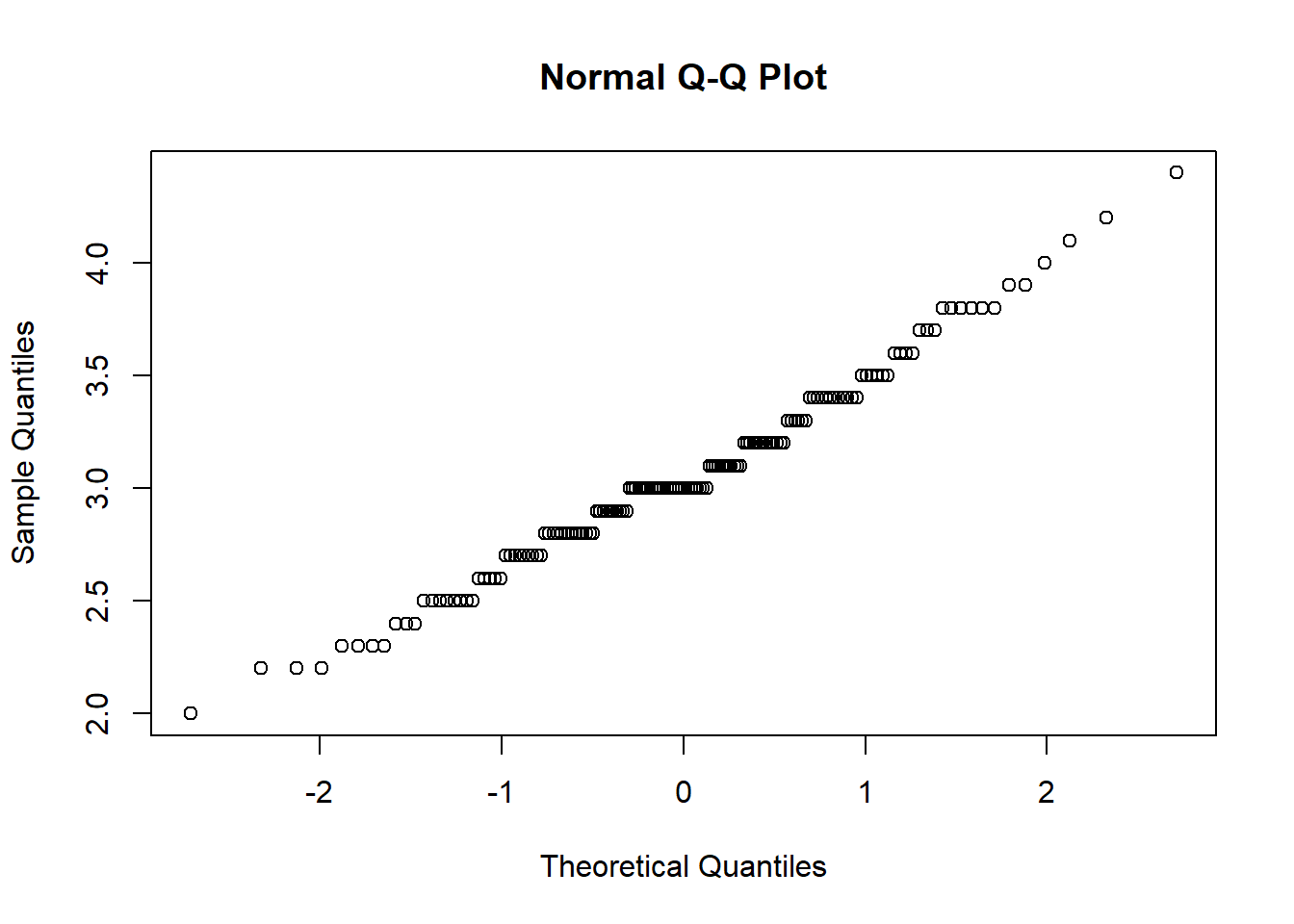
このようにほぼ一直線にデータが並んでおり、正規分布と見なしても構わないと言えます。念のためにシャピロ・ウィルクの正規性の検定を行うと
iris %>% with(., shapiro.test(x = Sepal.Width))##
## Shapiro-Wilk normality test
##
## data: Sepal.Width
## W = 0.98492, p-value = 0.1012
帰無仮説(H0:標本は正規母集団からサンプリングされたもの)が棄却されず、こちらからも正規分布であると言えます。
前述のように R のqqplot関数は正規分布だけでなく任意のデータ同士の分布を比較することができますので、これを用いて任意の二変量の分布を比較してみます。
データの正規化
QQプロットを描く前に比較対象となる二つのデータを正規化しておきます。正規化しても分布などは変わりません。
scale_vec <- function(x) { as.vector(scale(x)) }
(iris_norm <- iris %>% dplyr::select(-Species) %>%
dplyr::mutate_all(scale_vec)) %>%
GGally::ggpairs(diag = list(continuous = "barDiag"), progress = FALSE)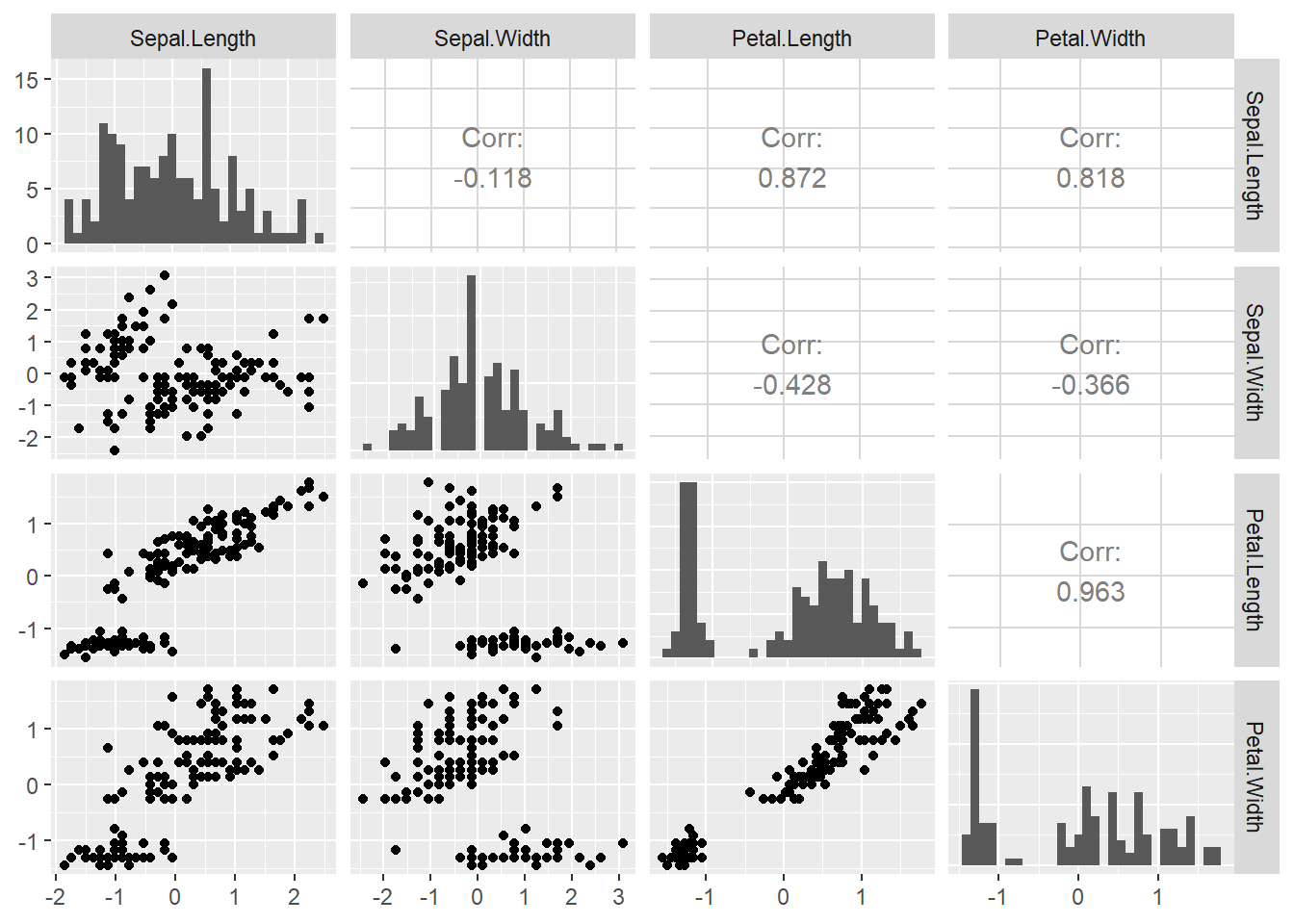
正規化はプロットした際にグラフを見やすくなるために行っています。
比較(Sepal.Width vs Sepal.Length)
まず「Sepal.WidthとSepal.Length」です。Sepal.Lengthが複数峰のように見えますが、これはヒストグラムの階級幅が原因のような気もします。
iris_norm %>% dplyr::select(Sepal.Width, Sepal.Length) %>%
GGally::ggpairs(diag = list(continuous = "barDiag"), progress = FALSE)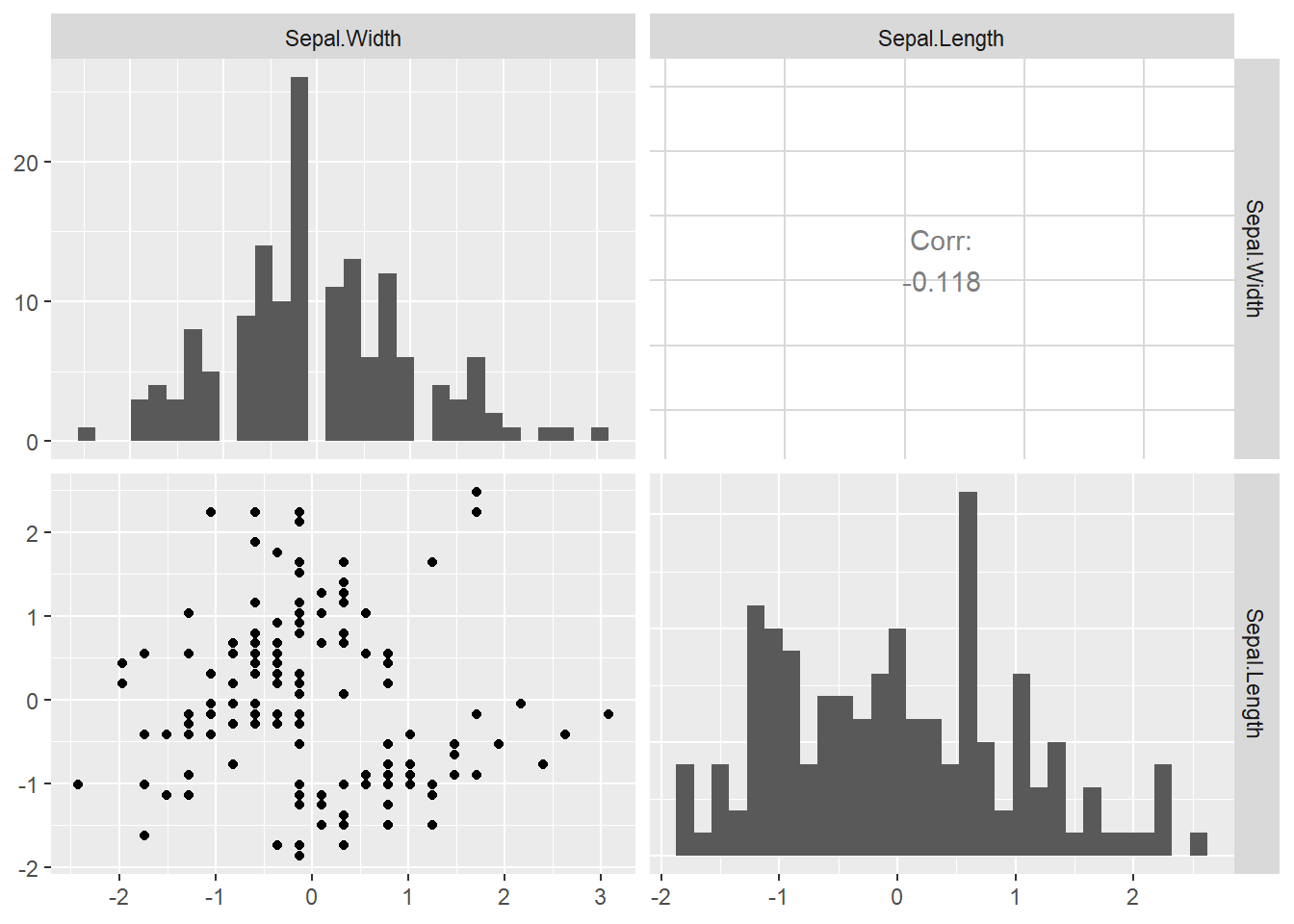
QQプロットを描いてみると両裾の部分で若干直線から外れているように見えますが、概ね一直線上にあり、二つの分布は等しいと言えるのではないでしょうか。
iris_norm %>% with(., qqplot(x = Sepal.Width, y = Sepal.Length))
abline(0, 1)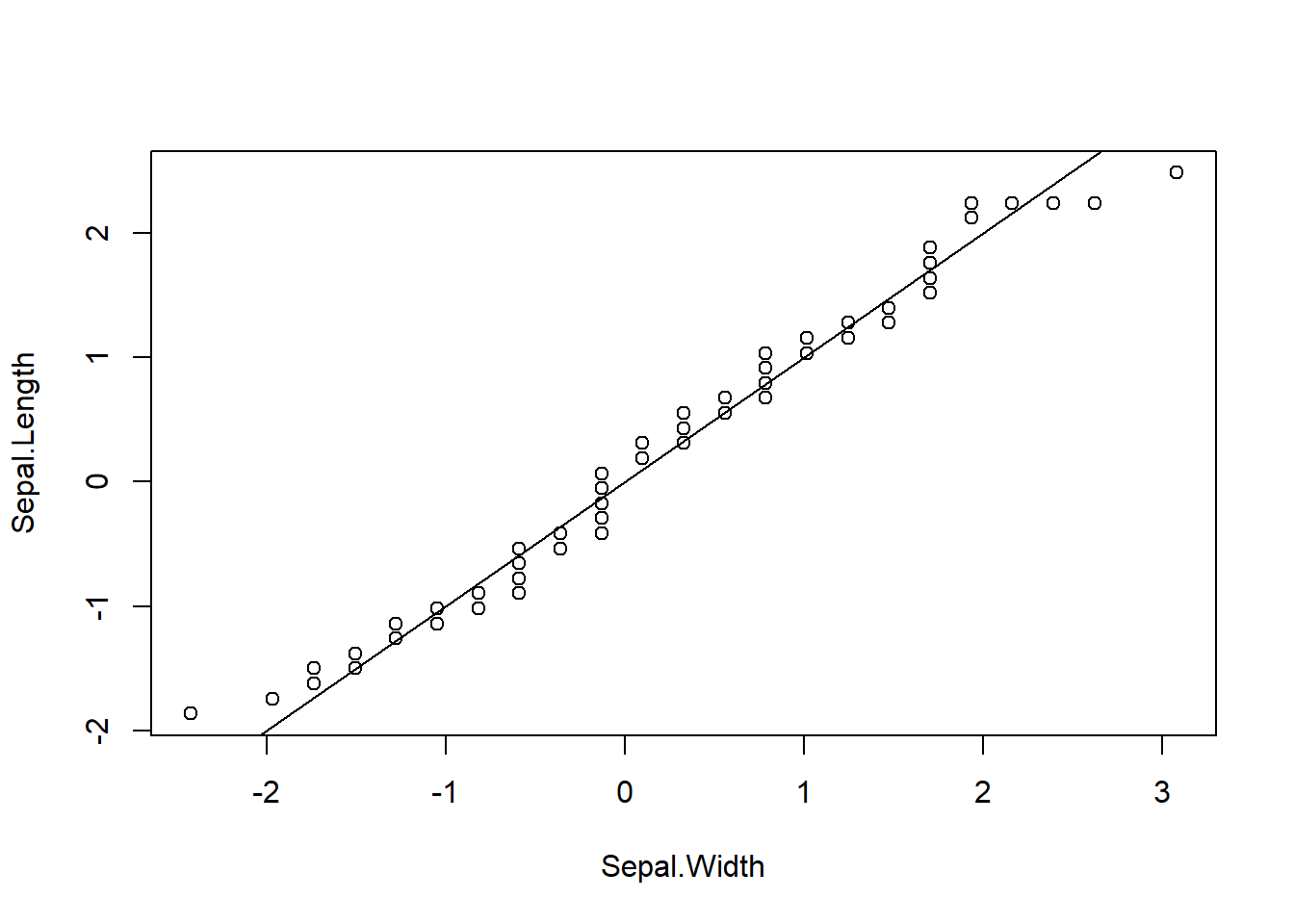
念のためにKS検定(コルモゴロフ-スミルノフ検定)を行うと帰無仮説(H0:二つの分布は等しい)は棄却されず、二つの分布は等しいと言えます。
iris_norm %>% with(., ks.test(Sepal.Width, Sepal.Length))## Warning in ks.test(Sepal.Width, Sepal.Length): p-value will be approximate
## in the presence of ties##
## Two-sample Kolmogorov-Smirnov test
##
## data: Sepal.Width and Sepal.Length
## D = 0.11333, p-value = 0.2904
## alternative hypothesis: two-sided
ただし、エラーメッセージにあるようにデータにタイ(同値)がありますのでp値は厳密な値ではない点に注意してください。
比較(Petal.Width vs Petal.Length)
次に「Petal.WidthとPetal.Length」を比較してみます。ニ峰の分布で概ね似たような分布に見えます。
iris_norm %>% dplyr::select(Petal.Width, Petal.Length) %>%
GGally::ggpairs(diag = list(continuous = "barDiag"), progress = FALSE)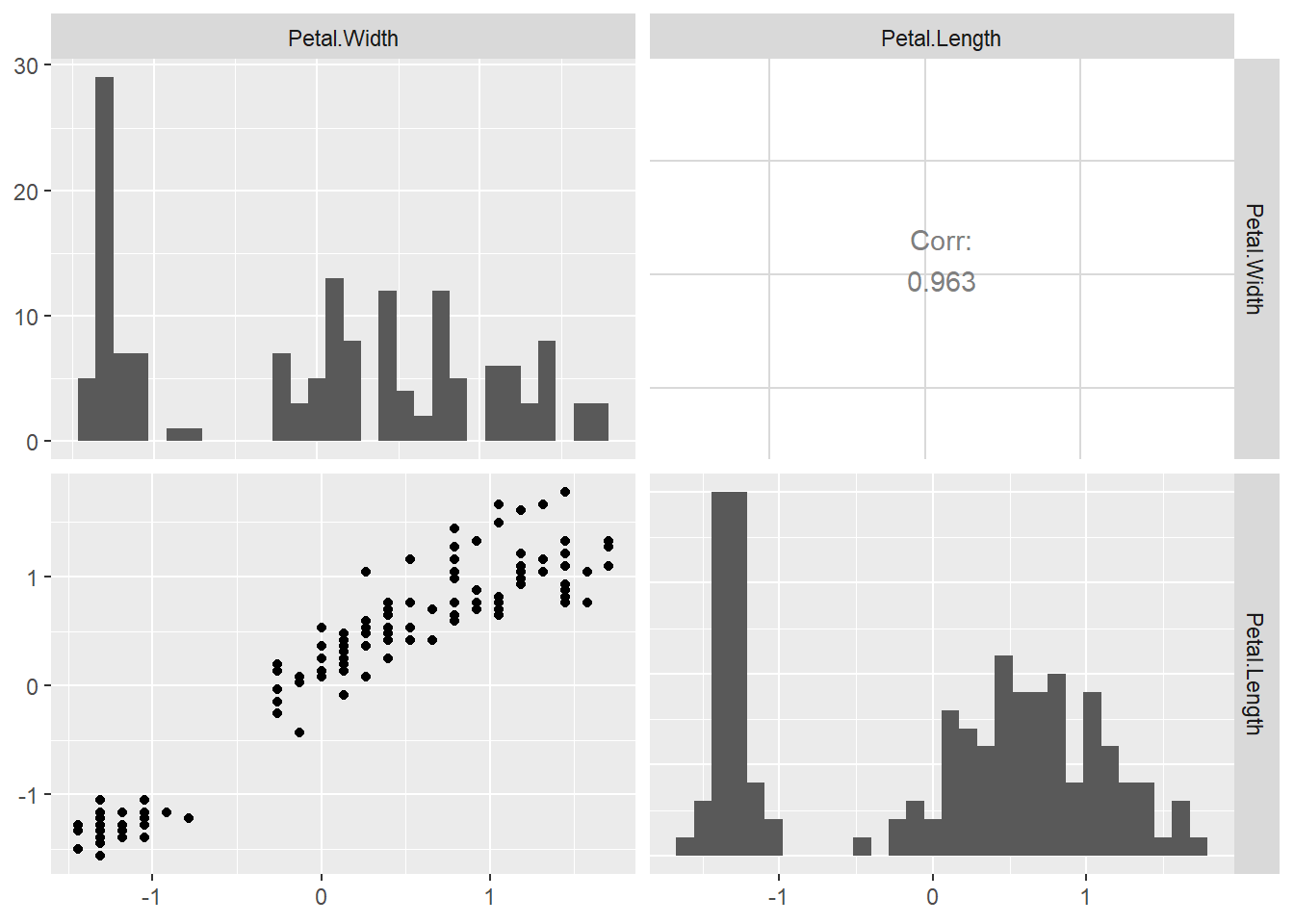
QQプロットを描いてみると概ね一直線上にあり二つの分布は等しいと言えるのではないでしょうか?
iris_norm %>% with(., qqplot(x = Petal.Width, y = Petal.Length))
abline(0, 1)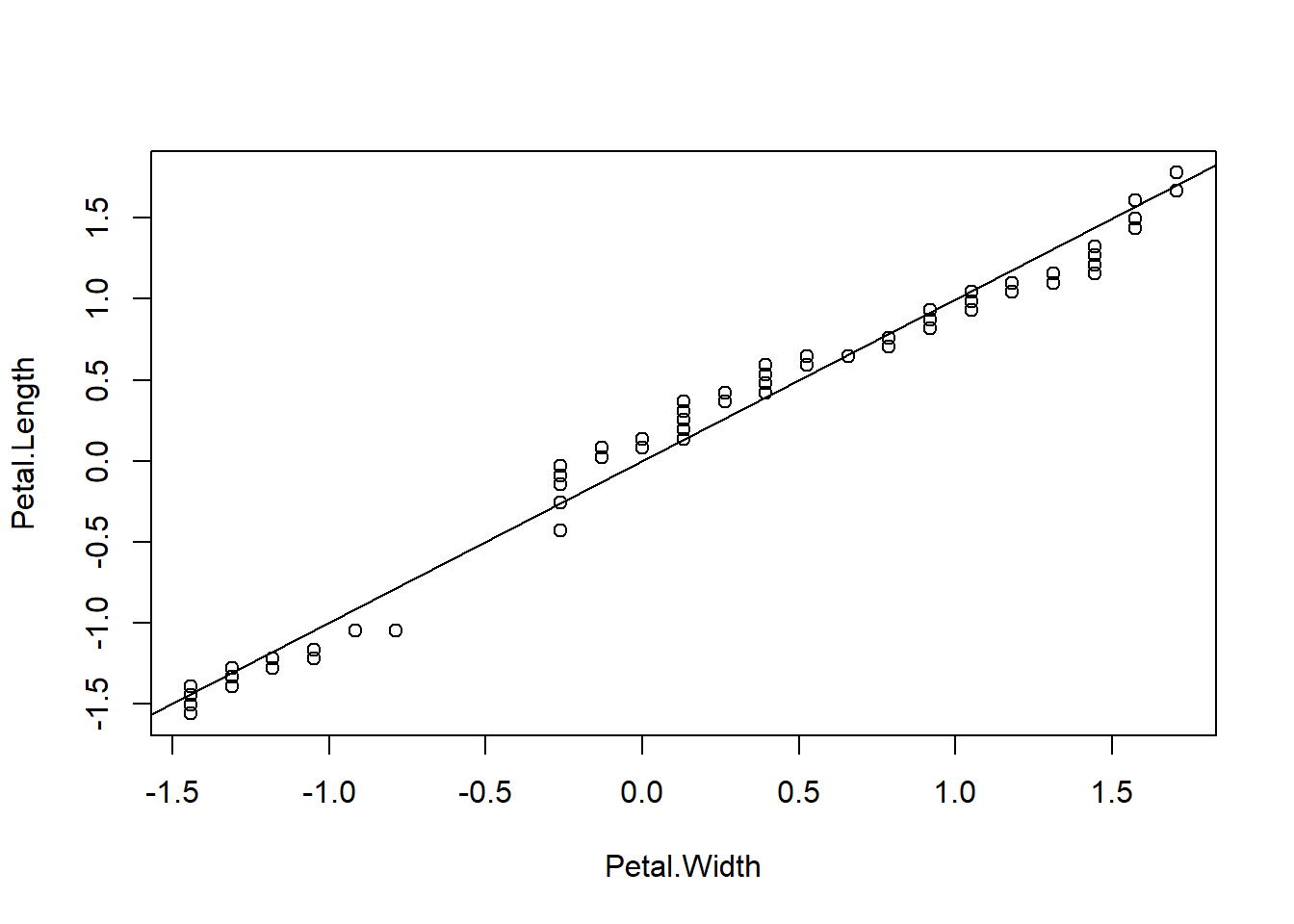
念のためにKS検定(コルモゴロフ-スミルノフ検定)を行うと帰無仮説(H0)は棄却されず、二つの分布は等しいと言えます。
iris_norm %>% with(., ks.test(Petal.Width, Petal.Length))## Warning in ks.test(Petal.Width, Petal.Length): p-value will be approximate
## in the presence of ties##
## Two-sample Kolmogorov-Smirnov test
##
## data: Petal.Width and Petal.Length
## D = 0.12667, p-value = 0.1801
## alternative hypothesis: two-sided
ただし、タイ(同値)の警告が出ている点は先ほどと同じです。
比較(Sepal.Width vs Petal.Length)
続いては、これは分布が同じとは言えないだろうと思われる「Sepal.WidthとPetal.Length」の比較です。
iris_norm %>% dplyr::select(Sepal.Width, Petal.Length) %>%
GGally::ggpairs(diag = list(continuous = "barDiag"), progress = FALSE)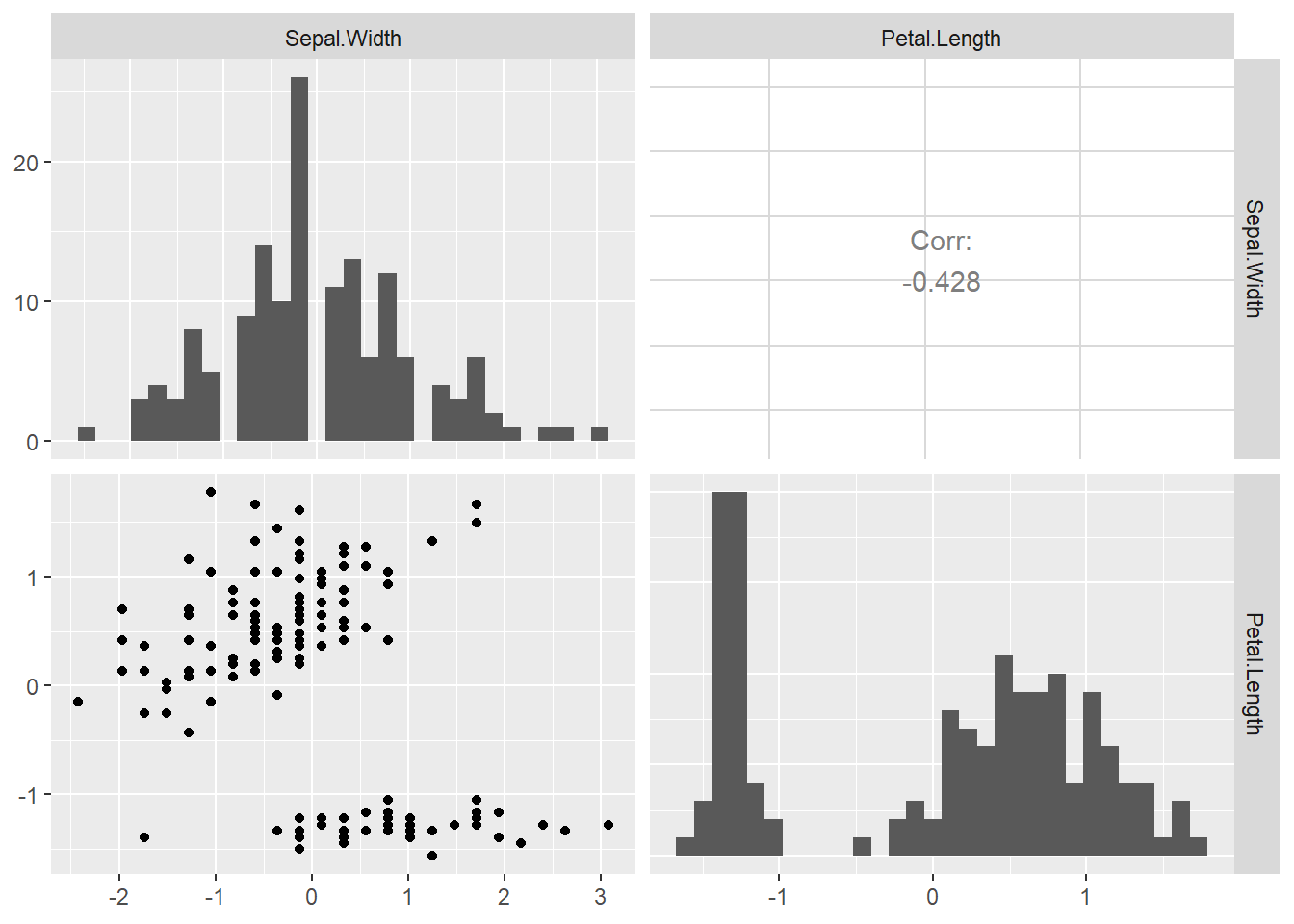
一応、QQプロットを描いてみると明らかに直線上にデータがありませんので、等しい分布とは言えません。
iris_norm %>% with(., qqplot(x = Sepal.Width, y = Petal.Length))
abline(0, 1)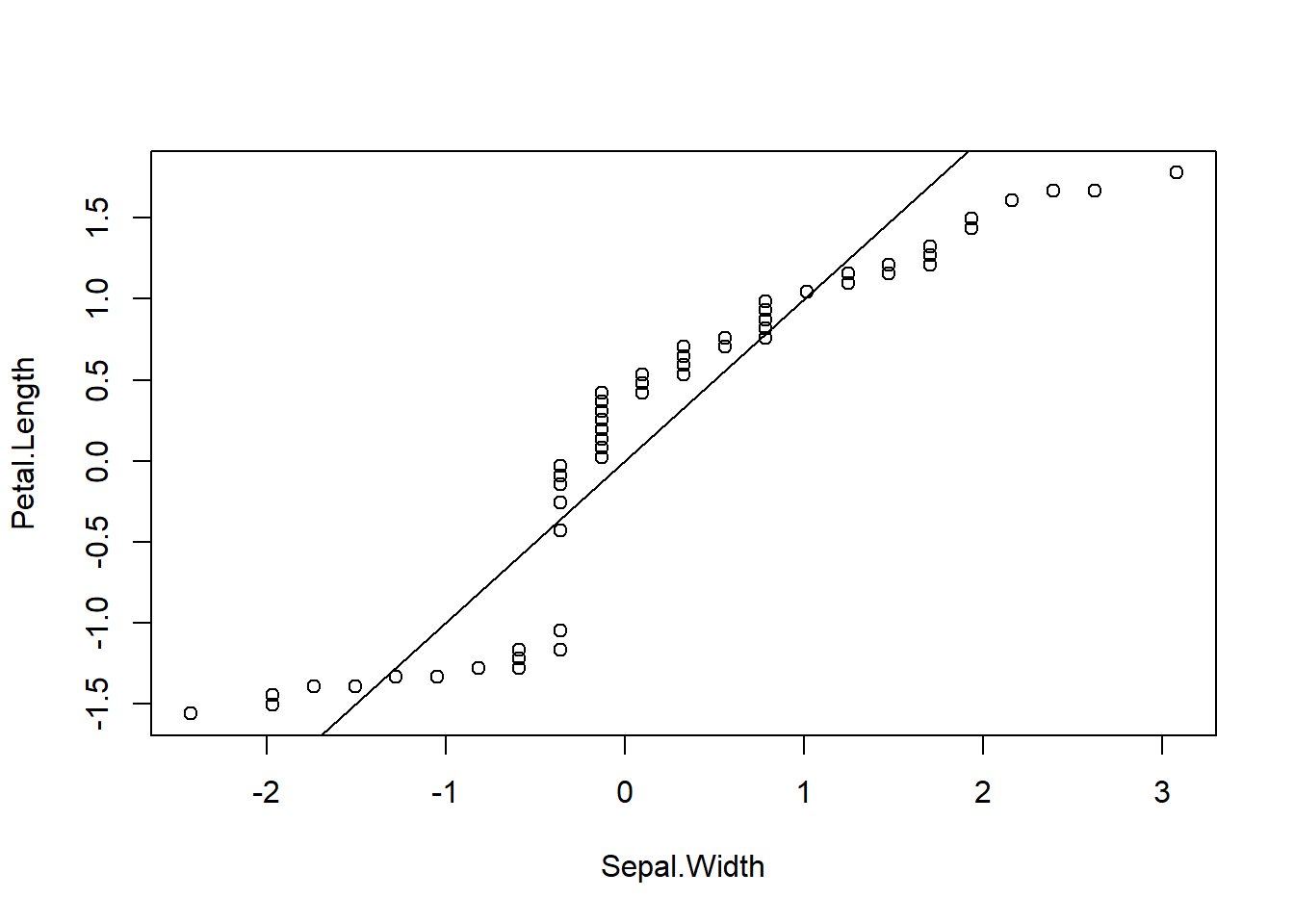
念のためにKS検定(コルモゴロフ-スミルノフ検定)を行うと帰無仮説(H0)は棄却さましたので、見た目通り等しい分布とは言えません。
iris_norm %>% with(., ks.test(Sepal.Width, Petal.Length))## Warning in ks.test(Sepal.Width, Petal.Length): p-value will be approximate
## in the presence of ties##
## Two-sample Kolmogorov-Smirnov test
##
## data: Sepal.Width and Petal.Length
## D = 0.22, p-value = 0.001406
## alternative hypothesis: two-sided
ただし、タイ(同値)の警告が出ている点は先ほどと同じです。
比較(Petal.Width vs Sepal.Length)
最後にこちらも同じ分布とは言えないだろうと思われる「Petal.WidthとSepal.Length」の比較です。
iris_norm %>% dplyr::select(Petal.Width, Sepal.Length) %>%
GGally::ggpairs(diag = list(continuous = "barDiag"), progress = FALSE)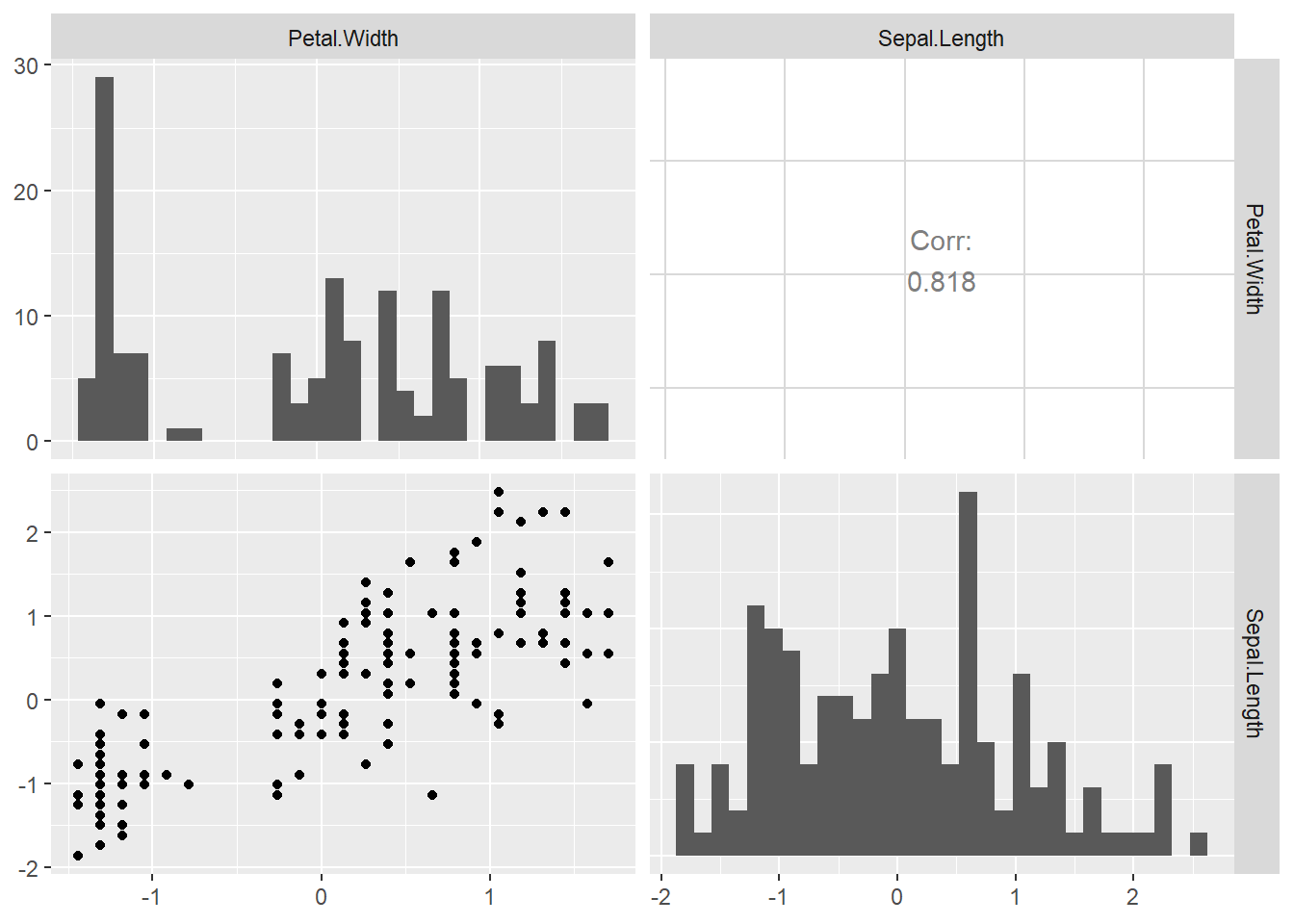
QQプロットを描いてみるとこちらも両裾の部分で直線から大きく外れている部分があります。
iris_norm %>% with(., qqplot(x = Petal.Width, y = Sepal.Length))
abline(0, 1)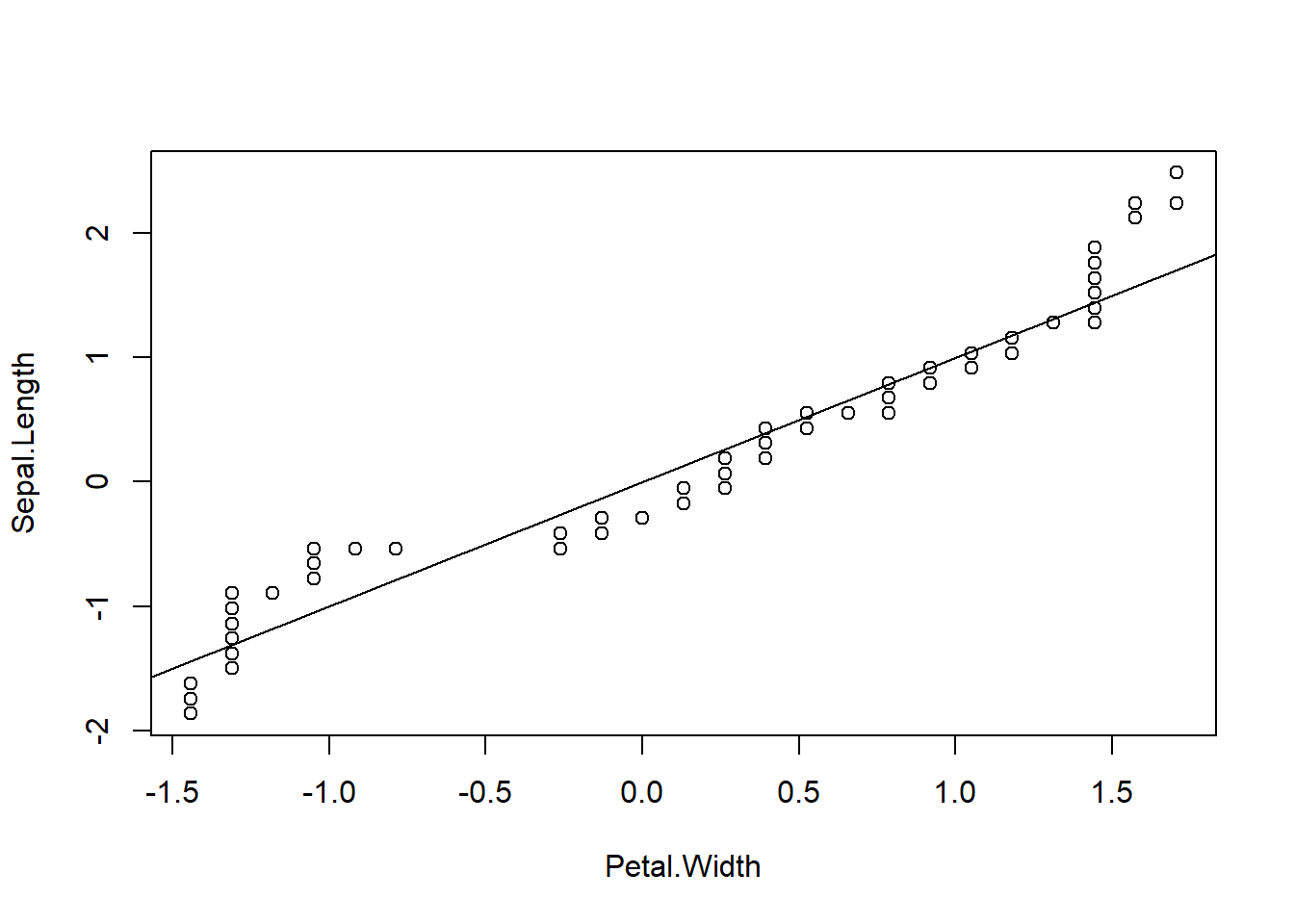
念のためにKS検定(コルモゴロフ-スミルノフ検定)を行うと帰無仮説(H0)は棄却さましたので、見た目通り等しい分布とは言えません。
iris_norm %>% with(., ks.test(Petal.Width, Sepal.Length))## Warning in ks.test(Petal.Width, Sepal.Length): p-value will be approximate
## in the presence of ties##
## Two-sample Kolmogorov-Smirnov test
##
## data: Petal.Width and Sepal.Length
## D = 0.17333, p-value = 0.02207
## alternative hypothesis: two-sided
ただし、タイ(同値)の警告が出ている点は先ほどと同じです。
おわりに
データの分布を見る場合にヒストグラムだと階級幅に左右されやすいので密度推定に基づく分布も見た方が良いかも知れません。
この分布ならばヒストグラムよりは納得感がありませんか?
Enjoy!